문제 링크
문제 요약
아래와 같은 이분 그래프가 주어집니다. 이때 간선들끼리 서로 교차하는 개수를 구하는 문제입니다.
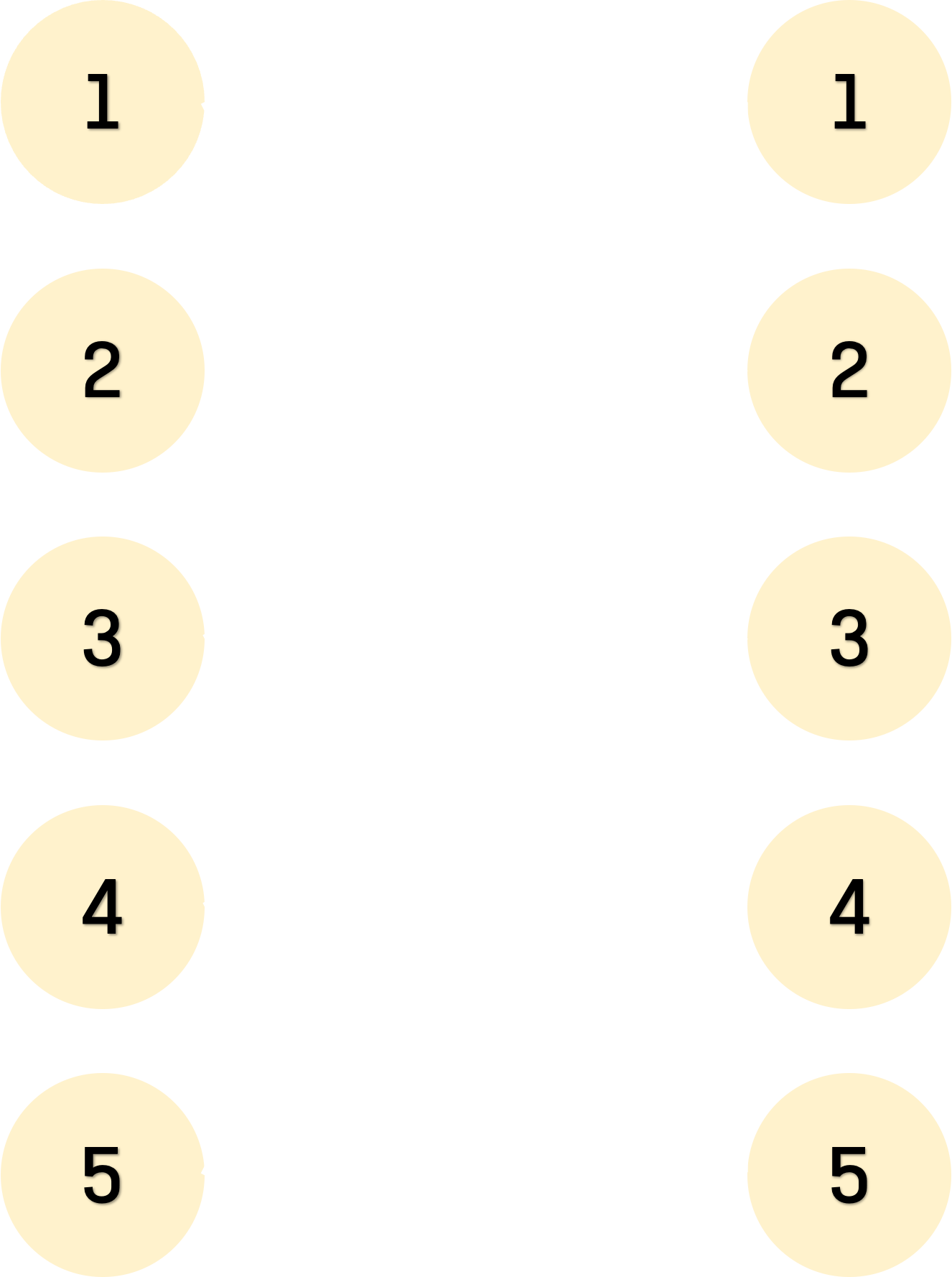
풀이
Segment Tree를 활용하면 쉽게 해결할 수 있습니다. 만약 Segment Tree를 모른다면 해당 페이지를 참고해주세요.
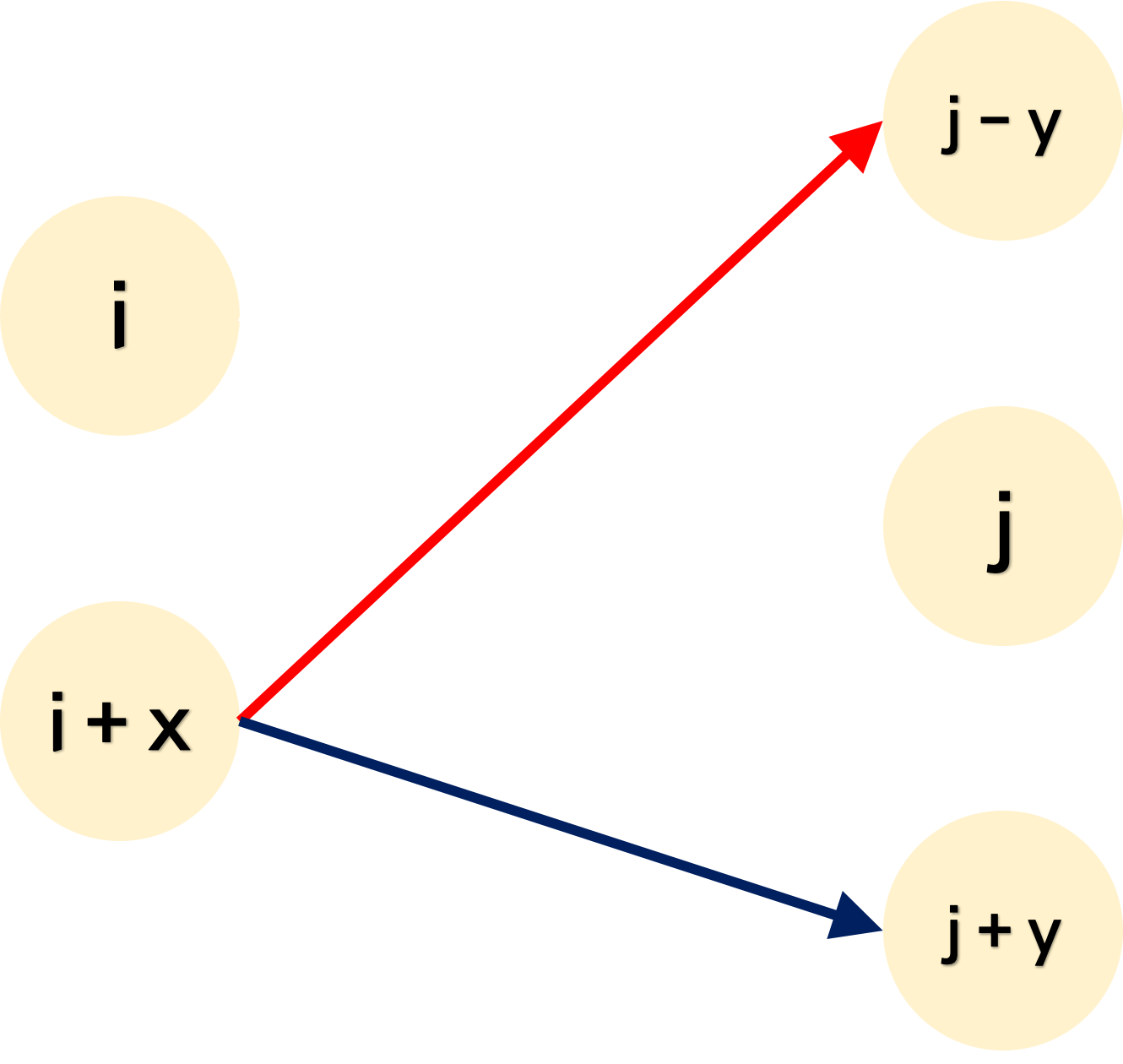
i → j 로 가는 상황의 간선이 있다고 가정해봅시다. 그리고 해당 간선과 교차되는 간선을 A 라고 해보겠습니다. 이때, A의 시작점이 i 보다 큰 상황이라면 A의 종료 지점은 j 보다 무조건 작아야 교차 지점이 생깁니다.
따라서 i에서 시작하는 간선에 대해 i보다 큰 지점에서 시작하는 간선들과 교차점이 있는지를 판단할 때, 현재 도착점 j 보다 작은 즉 1 ~ j - 1 까지 도착하는 간선의 수가 교차점의 개수가 됩니다. 그리고 이런 구간에 대한 쿼리는 Segment Tree를 안다면 구현할 수 있게 됩니다.
다만 주의할 것은 i에서 시작하는 간선이 하나가 아닐 수 있다는 점입니다. 이 때문에 살짝의 처리가 필요합니다. 아래 정답 코드에서 이 부분인데, 현재 i에서 시작하는 간선에 대해서 먼저 모든 개수를 삭제처리하고 쿼리하는 처리입니다.
forEachj(adj[i]) {
seg.update(j, j, -1);
}
forEachj(adj[i]) {
ans += seg.query(1, j-1);
}정답 코드
#include <bits/stdc++.h>
using namespace std;
#define for1(s, e) for(int i = s; i < e; i++)
#define for1j(s, e) for(int j = s; j < e; j++)
#define forEachj(k) for(auto j : k)
typedef long long ll;
typedef vector<ll> llv1;
typedef vector<llv1> llv2;
struct SegTree {
int n;
vector<ll> tree;
SegTree(int n) : n(n) {
tree.resize(4 * n + 5, 0);
}
void init(const vector<ll>& ar, int idx, int start, int end) {
if (start == end) {
tree[idx] = ar[start];
return;
}
int mid = (start + end) / 2;
init(ar, idx * 2, start, mid);
init(ar, idx * 2 + 1, mid + 1, end);
tree[idx] = tree[idx * 2] + tree[idx * 2 + 1];
}
void __update(int left, int right, int idx, ll val, int start, int end) {
if (end < left || start > right) return;
if(left <= start && end <= right) {
tree[idx] += val;
return;
}
int mid = (start + end) / 2;
__update(left, right, idx * 2, val, start, mid);
__update(left, right, idx * 2 + 1, val, mid + 1, end);
tree[idx] = tree[idx * 2] + tree[idx * 2 + 1];
}
ll __query(int left, int right, int idx, int start, int end) {
if (end < left || start > right) return 0;
if(left <= start && end <= right) {
return tree[idx];
}
int mid = (start + end) / 2;
ll l = __query(left, right, idx * 2, start, mid);
ll r = __query(left, right, idx * 2 + 1, mid + 1, end);
return l + r;
}
void update(int left, int right, ll val) {
__update(left, right, 1, val, 1, n);
}
ll query(int left, int right) {
return __query(left, right, 1, 1, n);
}
};
void solve() {
ll N, M, a, b;
llv2 adj;
llv1 ar;
ll ans = 0;
cin >> N >> M;
SegTree seg(N);
adj.resize(N + 1);
ar.resize(N + 1, 0);
for1(0, M) {
cin >> a >> b;
adj[a].push_back(b);
ar[b]++;
}
seg.init(ar, 1, 1, N);
for1(1, N+1) {
forEachj(adj[i]) {
seg.update(j, j, -1);
}
forEachj(adj[i]) {
ans += seg.query(1, j-1);
}
}
cout << ans;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(NULL);cout.tie(NULL);
int tc = 1; // cin >> tc;
while(tc--) solve();
}